In this instance, we'll explain the Gaussian fitting used in peak search analysis, one of the key features of our DSP and MCA spectrum analysis capabilities.

Techno AP's Gaussian fitting method for peak search employs a nonlinear least squares approach using the Levenberg-Marquardt method. This method ensures rapid convergence and stability, enabling precise determination of optimal values. Initial parameter values are automatically derived from peak search data, simplifying setup.

Here’s a straightforward explanation of the algorithm:

First, we work with spectral data y_i and a model function f(x_i;a), which consists of a Gaussian function plus a linear term.

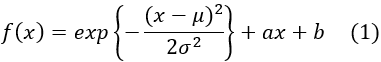
Let's unify the coefficient (parameter) of Eq.(1) with a.

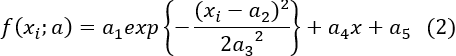
1. Give the independent variable x_i of the model function f(x_i;a) and set the initial value of the parametera a⁽⁰⁾.

2. Define χ2 (sum of weighted residual squares) Eq. (3) to evaluate the fit between data y_i and modelf(x_i;a) and calculate χ²(a⁽⁰⁾) . Let this value be χ₀².

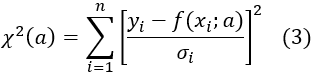
3. Create an m×m symmetric matrix α_jk by computing the partial derivatives of f(x_i;a) with respect to each parameter.

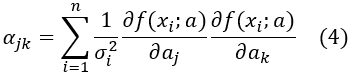
4. Create an m-by-1 matrixβ_j by multiplying the residual by partial differentiation.

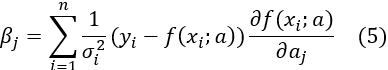
5. α' is obtained by multiplying the diagonal component α_jj by the coefficient to be emphasized (1+λ).

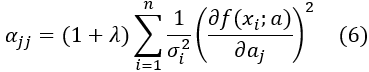
6. Solve the simultaneous equations Eq. (7) to find δa, and calculate χ2(a⁽⁰⁾+δa).

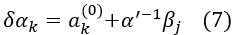
7.If χ²>χ₀², multiply λ by 10, and return to step 5 to try again.
8. If χ²-χ₀²<εχ², the calculation is complete. ε is the convergence criterion.
9. If χ²<χ₀², set a_j=a_j⁰,χ₀²=χ², set λ to 1/10, and return to step 3.

The Levenberg-Marquardt method initially increases λ during the first stage of fitting (when （a_j⁽⁰⁾ is not close to the true value), emphasizes the diagonal components, and causes the gradient of χ² to decrease sharply. In this case, since α_jj is large, the change in δα is small.

As χ² steadily decreases and λ approaches 0, the method moves the variation in δα more boldly, bringing it closer to Newton's method, allowing for rapid convergence.

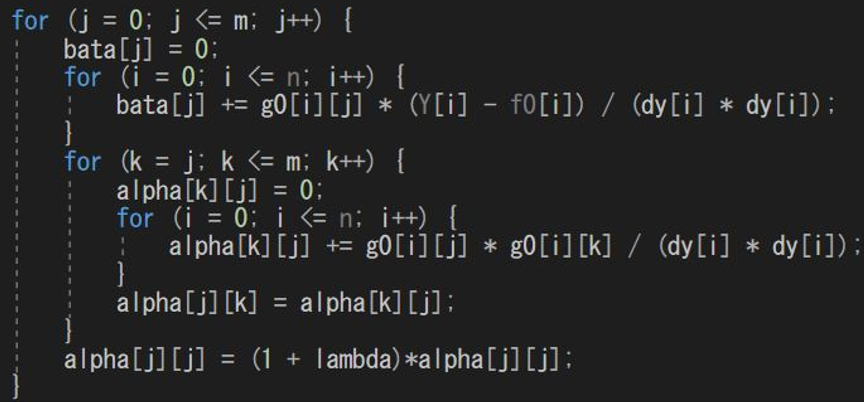
Fig.1 Gauss fitting code, part of the code

There are free libraries for nonlinear least squares methods like Gaussian fitting available for interpreted languages such as Python and ROOT, which excel at numerical computations.

Initially, I considered using these libraries, but since our application requires integration as a DLL, and paid options like Peak Fit and MATLAB support this, I realized we needed a custom solution.

Given the need for flexibility and customization, I opted to develop the solution in-house. Similar to our peak search functionality, this implementation is coded in C and compiled into a DLL (Fig. 1) ensuring high-speed performance and enabling real-time calculations.

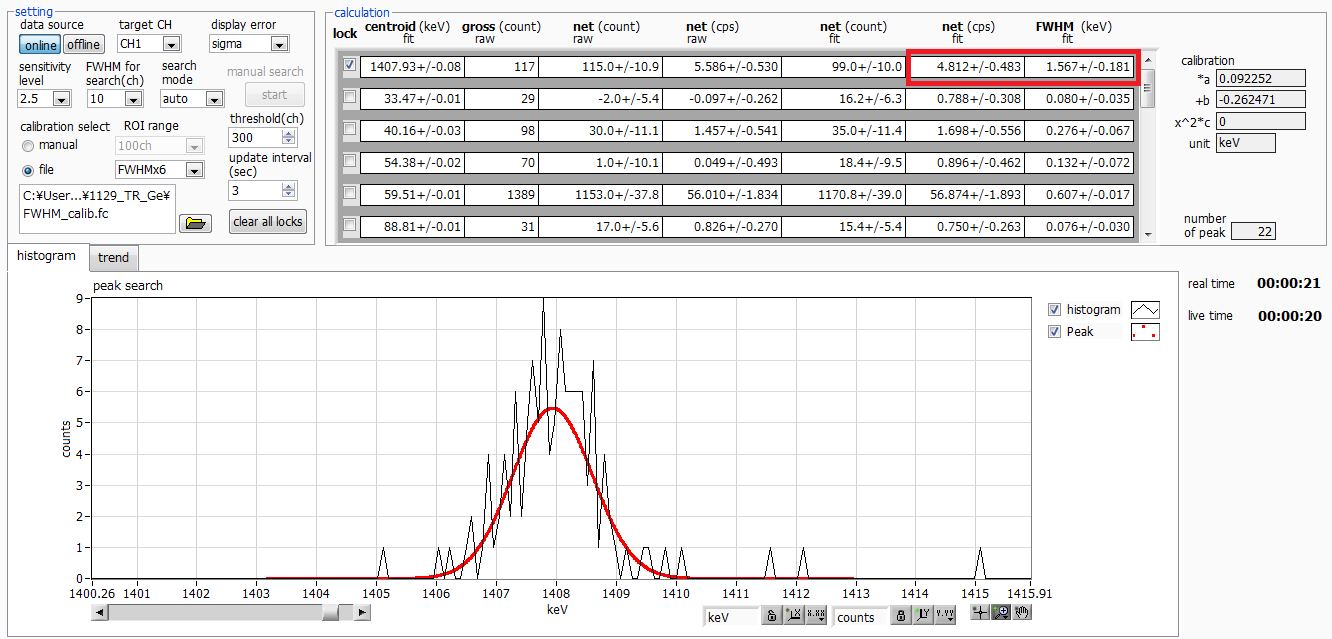
Fig.2 Spectrum with few statistics

Firstly, Gaussian fitting offers the advantage that it can provide reasonable values (Fig. 2) even when statistical data is limited (Fig. 3). Its high reproducibility ensures stable results without the need for extended measurement periods.

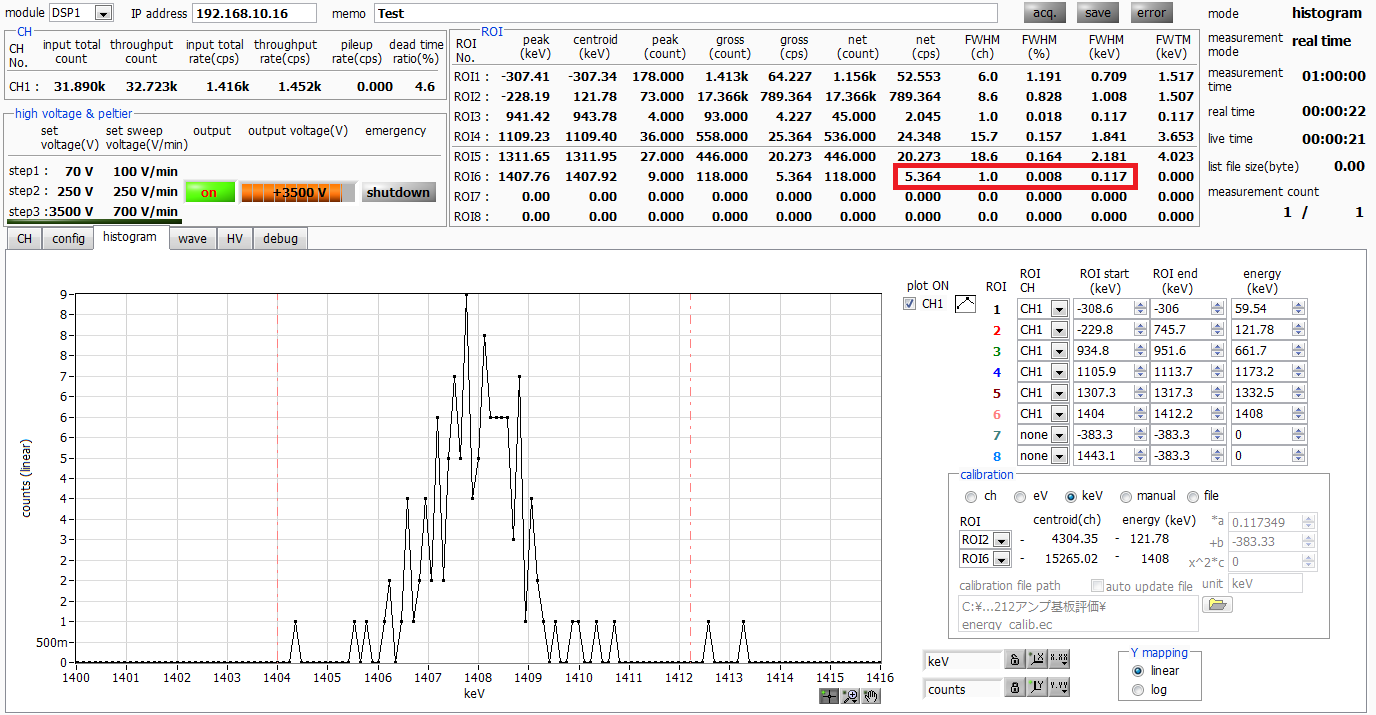
Fig.3 Manual calculation process on main screen

Additionally, when the full scale is set broadly, such as 10 MeV (Fig. 4), and focus is on lower energies (e.g., 121.8 keV), fine binning with 16 kch histogram channels may lead to inadequate channel resolution (Fig. 5).

The value net(cps)raw, derived from direct measurements, often proves smaller than net(cps)fit calculated via Gaussian fitting. This discrepancy is likely due to insufficient channel resolution. Gaussian fitting remains effective in such scenarios.

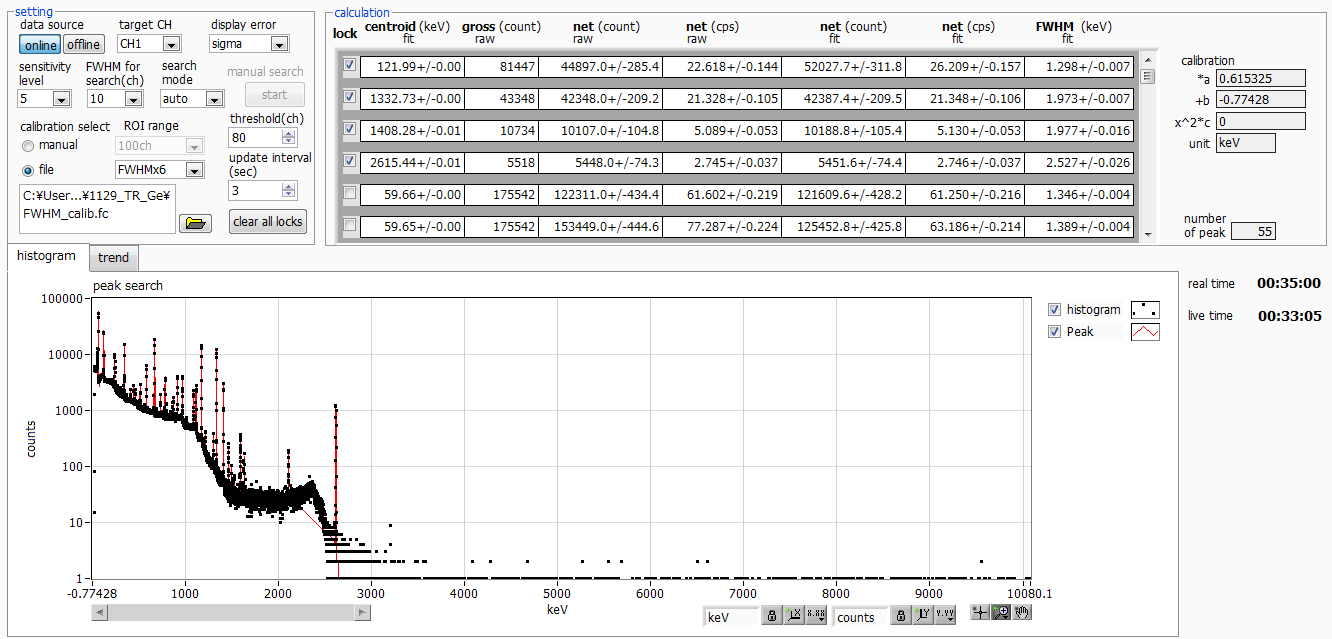
Fig.4 10MeV full-scale γ-ray spectrum

Fig.5 Spectrum with insufficient channel resolution

Although the application automatically derives initial values from peak search results and applies Gaussian fitting accordingly, rendering manual intervention unnecessary, real-time updates of information add significant utility.

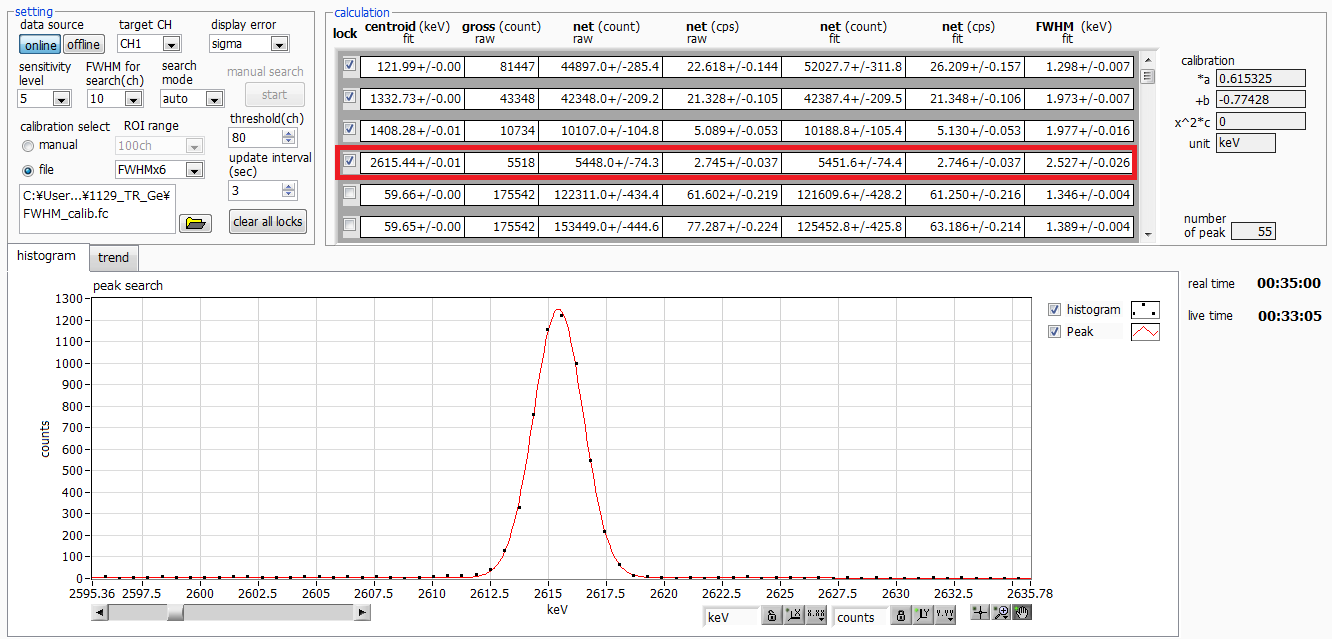
Fig.6 2.6MeV peak

Fig.6 shows the peak of the 2.6 MeV γ-ray of Tl-208 from the natural radiation thorium series generated by the thorium-containing tungsten electrode rod used in circulating TIG welding.
This is useful when testing high-energy gamma rays.

Fig.7 is a spectrum measured for 35 minutes at a full scale of 3MeV.
Please pay attention to the blue frame.

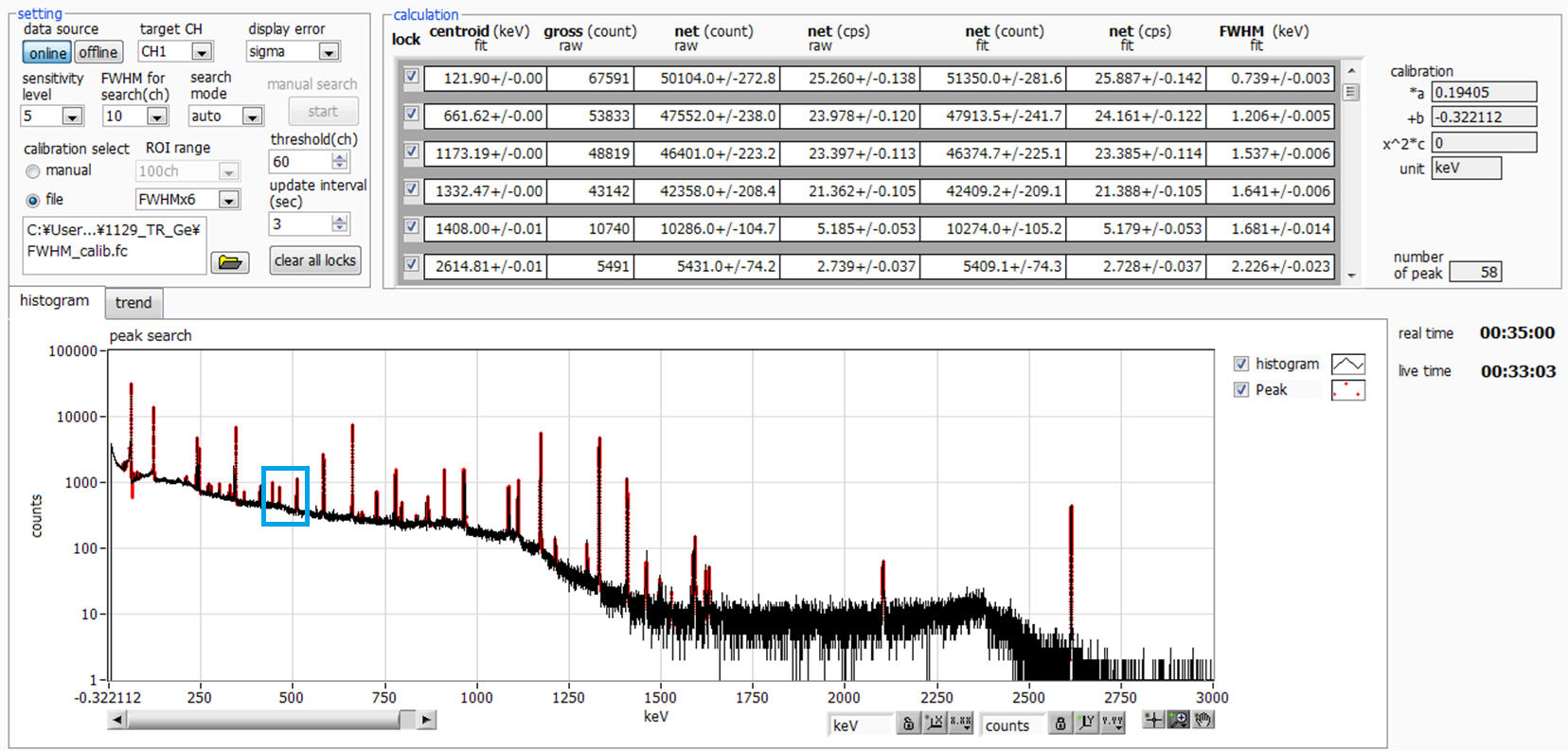
Fig.7 3MeV full-scale γ-ray spectrum

Fig.8 shows the spectrum with the blue frame enlarged. Measured for 1 minute. 443keV and 463keV seem to be still hidden,

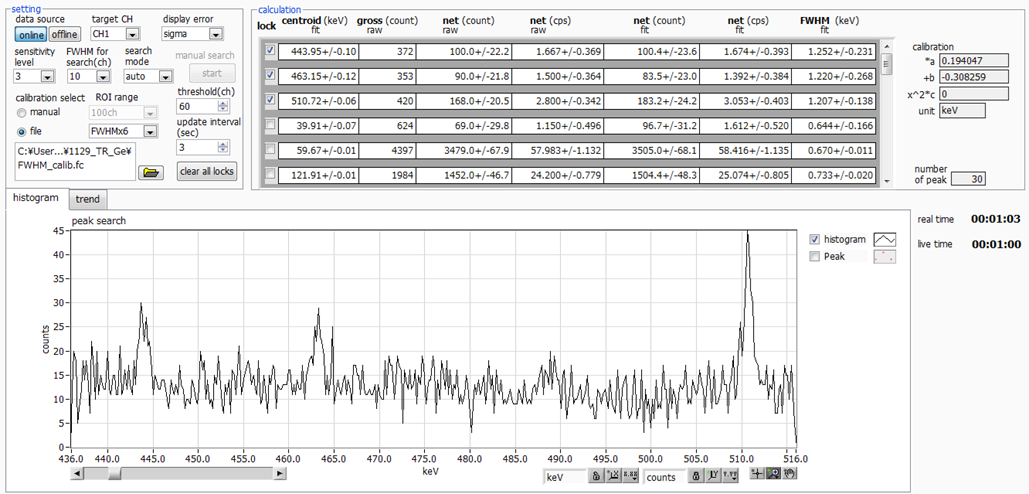
Fig.8 Peak that is slightly buried

Gauss fitting is applied properly. (Fig.9)

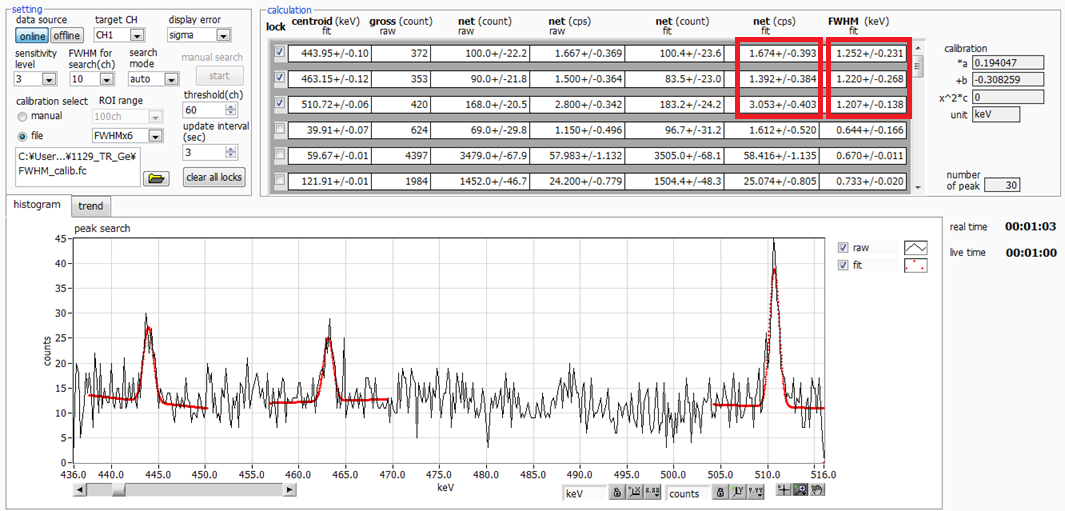
Fig.9 1 minute measurement of the fitted spectrum

Compare the three peaks in the 1min spectrum (Fig.9) and 10min spectrum (Fig.10).
I believe net(cps)fit and FWHM(keV)fit are within the error range.

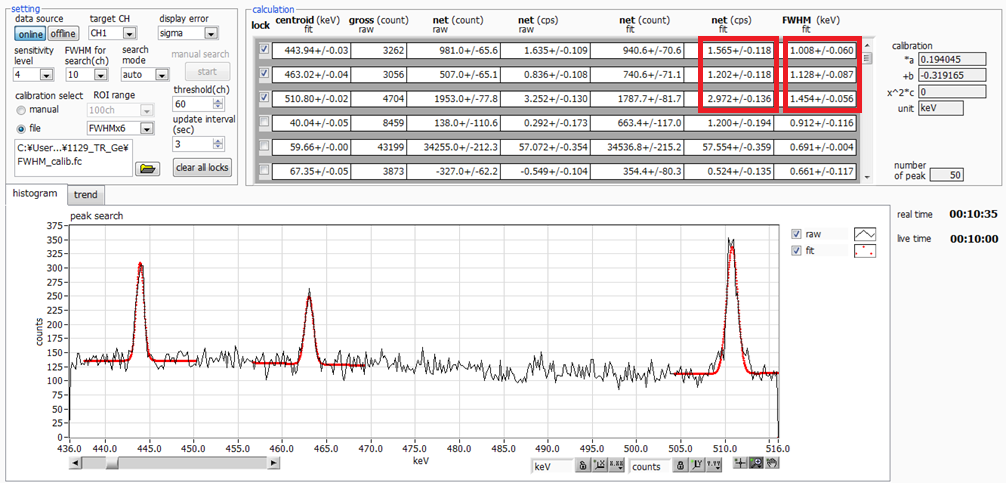
Fig.10 Spectrum 10min measurement with fitting

All of our employees will do their best to create even better products.
Thank you very much for your support.

References
[1] Willaim H. Press, NUMERICAL RECIPES in C, (Gijutsu-Hyoron Co., Ltd., 1993)